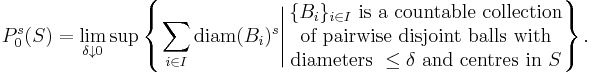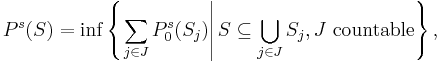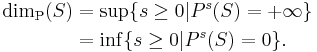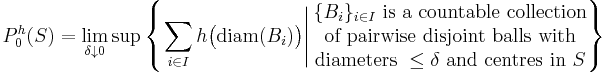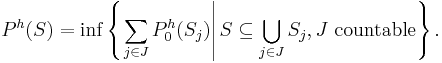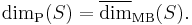Packing dimension
In mathematics, the packing dimension is one of a number of concepts that can be used to define the dimension of a subset of a metric space. Packing dimension is in some sense dual to Hausdorff dimension, since packing dimension is constructed by "packing" small open balls inside the given subset, whereas Hausdorff dimension is constructed by covering the given subset by such small open balls.
Contents |
Definitions
Let (X, d) be a metric space with a subset S ⊆ X and let s ≥ 0. The s-dimensional packing pre-measure of S is defined to be
Unfortunately, this is just a pre-measure and not a true measure on subsets of X, as can be seen by considering dense, countable subsets. However, the pre-measure leads to a bona fide measure: the s-dimensional packing measure of S is defined to be
i.e., the packing measure of S is the infimum of the packing pre-measures of countable covers of S.
Having done this, the packing dimension dimP(S) of S is defined analogously to the Hausdorff dimension:
Generalizations
One can consider dimension functions more general than "diameter to the s": for any function h : [0, +∞) → [0, +∞], let the packing pre-measure of S with dimension function h be given by
and define the packing measure of S with dimension function h by
The function h is said to be an exact (packing) dimension function for S if Ph(S) is both finite and strictly positive.
Properties
- If S is a subset of n-dimensional Euclidean space Rn with its usual metric, then the packing dimension of S is equal to the upper modified box dimension of S:
- This result is interesting because it shows how a dimension derived from a measure (packing dimension) agrees with one derived without using a measure (the modified box dimension).
Note, however, that the packing dimension is not equal to the box dimension. For example, the set of rationals Q has box dimension one and packing dimension zero.
See also
References
- Tricot, Jr., Claude (1982). "Two definitions of fractional dimension". Math. Proc. Cambridge Philos. Soc, 91 (1): 57–74. doi:10.1017/S0305004100059119. MR633256